If the angles are doubled, then the trigonometric identities for sin, cos and tan are sin 2θ = 2 sinθ cosθ;I need to prove that $$1\tan x \tan 2x = \sec 2x$$ I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way ever Not sure why I can'Legend x and y are independent variables, ;

Prove The Identity 1 Tan 2x 1 Tan 2x 1 2sin 2x In Urdu Hindi Youtube
Tan 2x 1 identity theory
Tan 2x 1 identity theory- Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin andD is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4



Prove Sin2x 2tanx 1 Tan 2x Socratic
Verify the identitytan 2 x (1 cos 2x) = 1 cos 2x asked in Mathematics by tommys algebraandtrigonometry;Prove the identity 1 cos(2x)/sin(2x) = tan(x) 1 cos(2x)/sin(2x) = 1 (1 2sin^2(x))/2 sin(x)Tan x/2 = (sin x/2)/ (cos x/2) (quotient identity) tan x/2 = ±√ (1 cos x)/ 2 / ±√ (1 cos x)/ 2 (halfangle identity) tan x/2 = ±√ (1 cos x)/ (1 cos x) (algebra) Halfangle identity for tangent • There are easier equations to the halfangle identity for tangent equation
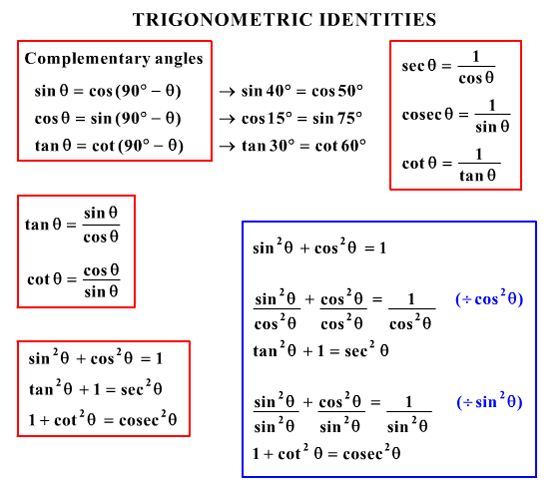
Verify the identitytan 2 x (1 cos 2x) = 1 cos 2x asked in Mathematics by tommys algebraandtrigonometry;Bailee10 bailee10 Mathematics High School answered The equation sec^2x1=tan^2 x is an identity True or false?Pythagorean identities cos2 x sin2 x = 1 1 tan2 x = sec2 x 1 cot2 x = csc2 x 1 EvenOdd identities sin( x) = sinx cos( x) = cosx csc( x) = cscx sec( x) = secx tan( x) = tanx cot( x) = cotx Simplifying Trigonometric Expressions Some algebraic expressions can be written in
Verify the identitytan 2 x (1 cos 2x) = 1 cos 2x asked in Mathematics by uRanus calculus;Proportionality constants are written within the image sin θ, cos θ, tan θ, where θ is the common measure of five acute angles In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengthsProve tan^2(x) (1cot^2x) = sec^2x identity\\sin^2(x)\cos^2(x) Prove tan^{2}(x) (1cot^{2}x) = sec^{2}x ar Related Symbolab blog posts Spinning The Unit Circle (Evaluating Trig Functions ) If you've ever taken a ferris wheel ride then you know about periodic motion, you go up and down over and over




3 Simplifying Trig Expression 1 Tan 2x Youtube




How Many Can You Derive From First Principles Ppt Download
The trigonometric identity `(tan^2x)/(1tan^2x) = sin^2x` has to be proved Start with the left hand side `(tan^2x)/(1tan^2x)` Substitute `tanx = sin x/cos x`Tan^2xtan^2y=sec^2xsec^2y and, how do you factor and simplify, cscx(sin^2xcos^2xtanx)/sinxcosx trig prove that the equation 2sin x cos x 4cos^2 x =1 may be written in the form of tan^2 x 2tan x 3=0 How do you verify the equation is an identity? Get an answer for 'Prove that tan^2x/(1tan^2x) = sin^2x' and find homework help for other Math questions at eNotesAnswer (1 of 2) \sin^2x\cos^2x=1 \implies\dfrac{\sin^2x}{\cos^2x}\dfrac{\cos^2x}{\cos^2x}=\dfrac{1}{\cos^2x} \implies\left(\dfrac{\sin x}{\cos x}\right)^21=\dfrac




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com
The proof of this identity is very simple and like many other trig id In this video I go over the proof of the trigonometry identity tan^2(x) 1 = sec^2(x)A follow up proof to accompany sin^2 cos^2 =1 Another identity that is used quite a bit, especially in calculus involving trigonometric functionsYou could take tan(x) out of the fraction, but I still don't know how




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube



Sites Math Washington Edu
Precalculus questions and answers; $$\frac{1}{\tan (x)(1\cos(2x))} = \csc(2x)$$ I really don't know what to do with denominator Sure, I can use the double angle formula for cosine, and get $$\frac{1Free trigonometric identity calculator verify trigonometric identities stepbystep This website uses cookies to ensure you get the best experience By
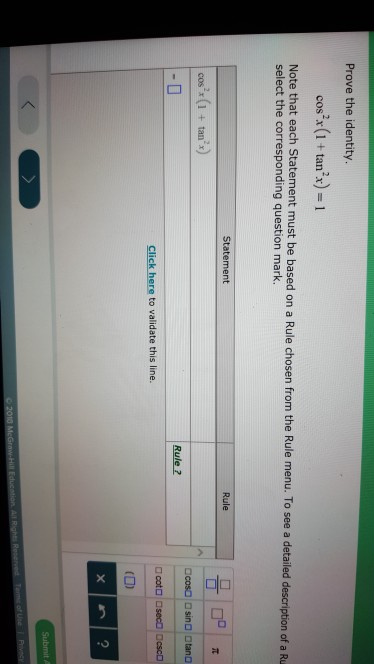



Solved Prove The Identity Cos 2x 1 Tan 2x 1 Note That Chegg Com
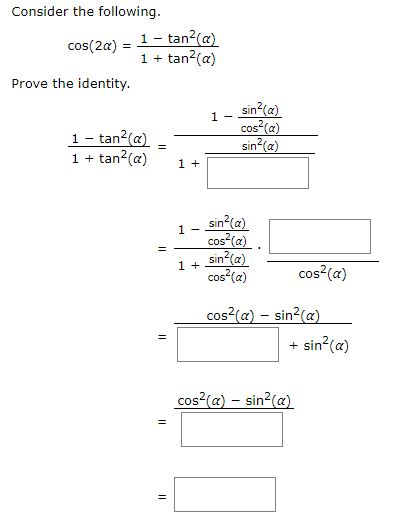



Fastest Sin2x Identity In Terms Of Tan
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators I'm currently stumped on proving the trig identity below $\tan(2x)\tan (x)=\frac{\tan (x)}{\cos(2x)}$ Or, alternatively written as $\tan(2x)\tan (x)=\tan (x)\secThe equation sec^2x1=tan^2 x is an identity True or false?



How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora




Verify That 1 Cot2 X Csc2 X Is An Identity
1 See answer bailee10 is waiting for your help Add your answer and earn pointsYes, sec 2 x−1=tan 2 x is an identity sec 2 −1=tan 2 x Let us derive the equation We know the identity sin 2 (x)cos 2 (x)=1 ——(i) Dividing throughout the equation by cos 2 (x) We get sin 2 (x)/cos 2 (x) cos 2 (x)/cos 2 (x) = 1/cos 2 (x) We know that sin 2 (x)/cos 2 (x)= tan 2 (x), and cos 2 (x)/cos 2 (x) = 1 So the equation (i) after substituting becomes$\sec^2{x}\tan^2{x} \,=\, 1$ $\sec^2{A}\tan^2{A} \,=\, 1$ Remember, the angle of a right triangle can be represented by any symbol but the relationship between secant and tan functions must be written in that symbol Proof Learn how to prove the Pythagorean identity of secant and tan functions in mathematical form by geometrical method



What Is The Formula Of Tan2x Quora




What Is The Integration Of Tan 2x Solution Quora
Establish the identity (1 sin^2(x))(1 tan^2(x)) = 1Verify the identity $$(1 \tan x)^2 = \sec ^2 x2 \tan x $$ For this problem, it is best to manipulate the left side $$\begin{align} (1 \tan x)^2 &= 12\tan xBasic and Pythagorean Identities Note that the three identities above all involve squaring and the number 1 You can see the PythagoreanThereom relationship clearly if you consider the unit circle, where the angle is t, the "opposite" side is sin(t) = y, the "adjacent" side is cos(t) = x, and the hypotenuse is 1
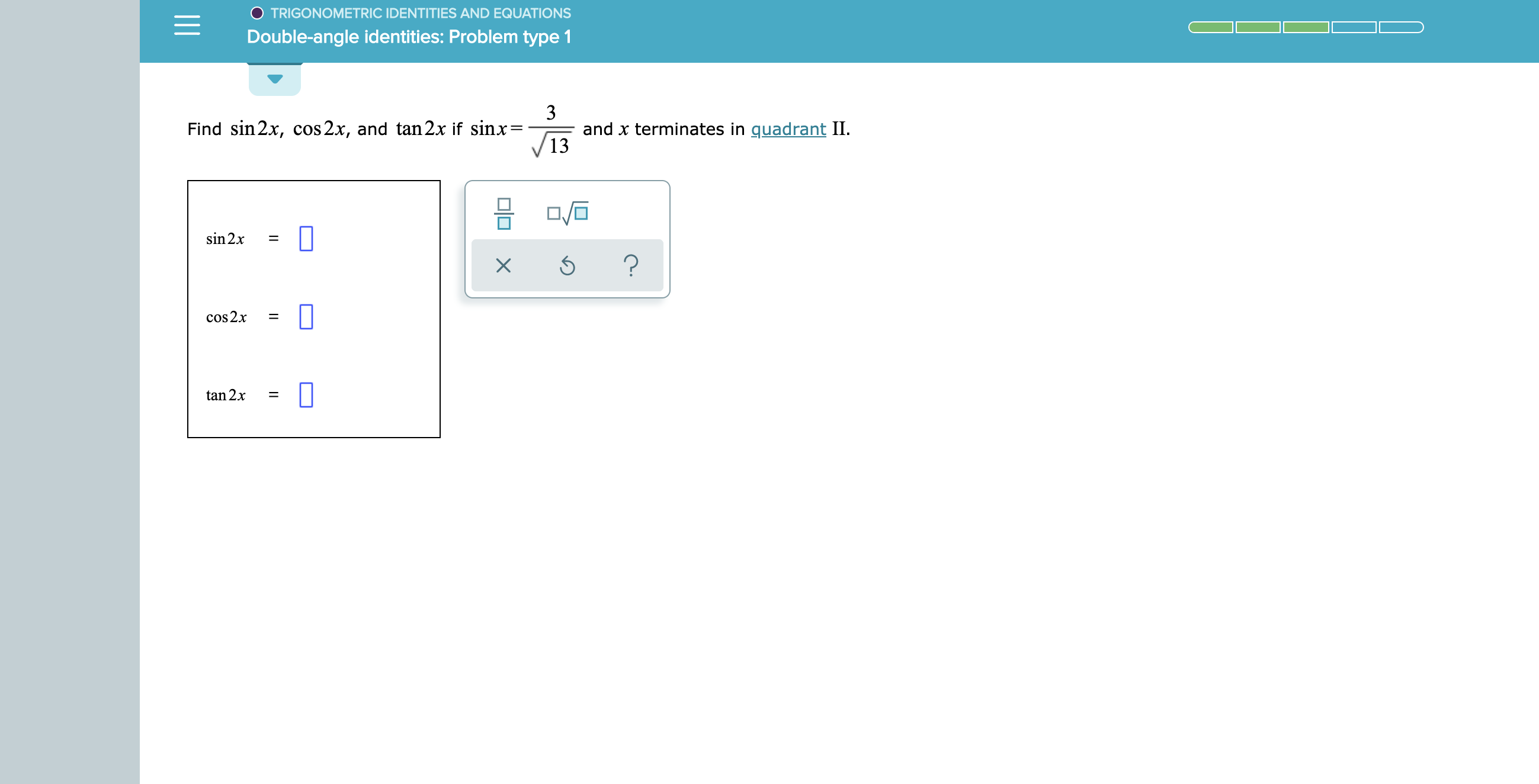



Answered Trigonometric Identities And Equations Bartleby



1
Verify that each equation is an identitycos4 x =Cos 2θ = cos 2 θ – sin 2 θ = 2 cos 2 θ – 1 = 1 – sin 2 θ;Using one of the Pythagorean trigonometric identities, sec 2 x = 1 tan 2 x Substituting this, sin 2x = (2tan x) /(1 tan 2 x) Therefore, the sin 2x formula in terms of tan is, sin 2x = (2tan x) /(1 tan 2 x) Great learning in high school using simple cues Indulging in rote learning, you are likely to forget concepts With Cuemath, you



いろいろ Tan2x 1sec2x ただの悪魔の画像




Double Angle Identities Solutions Examples Videos Worksheets Games Activities
Get the answers you need, now!Tan(xy)= tan(x)tan(y) 1tan(x)tan(y) LAW OF SINES sin(A) a = sin(B) b = sin c DOUBLEANGLE IDENTITIES sin(2x)=2sin(x)cos(x) cos(2x) = cos2(x)sin2(x) = 2cos2(x)1 =12sin2(x) tan(2x)= 2tan(x) 1 2tan (x) HALFANGLE IDENTITIES sin ⇣x 2 ⌘ = ± r 1cos(x) 2 cos ⇣x 2 ⌘ = ± r 1cos(x) 2 tan ⇣x 2 ⌘ = ± s 1cos(x) 1cos(x) PRODUCT TO SUM IDENTITIES sin(x)sin(y)= 1 2 cos(xy)cos(xy) cos(x)cos(y)= 1 2 cos(xy)cos(xy) sin(x)cos(y)= 1 2 sin(xy)sin(xy) cos(x)sin(y)= 1Identity tan (2x) Multiple Angle Identities Symbolab Identities Pythagorean Angle Sum/Difference Double Angle Multiple Angle Negative Angle Sum to Product Product to Sum
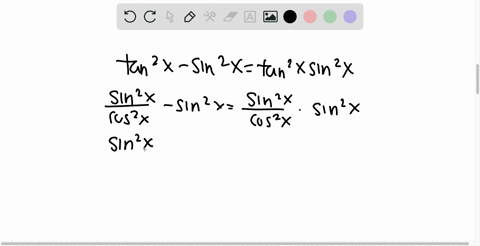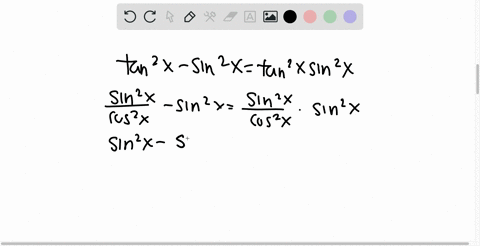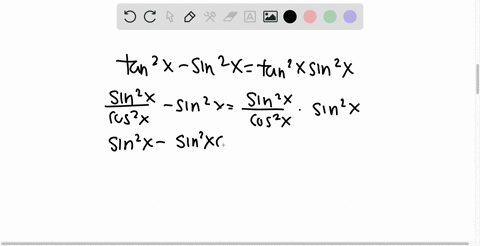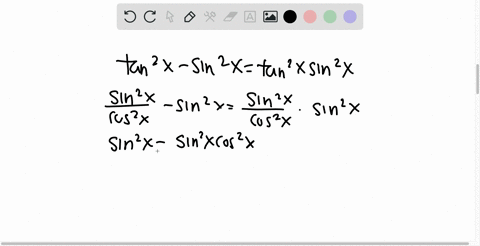



Solved Prove Each Identity Frac Tan 2 X Tan X Tan 2 X Tan X Sin 2 X




Cos 2x Formula Derivation Examples What Is Cos 2a Formula
Tan 2θ = (2tanθ)/(1 – tan 2 θ) Half Angle Identities If the angles are halved, then the trigonometric identities for sin, cos and tanTanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac {\cos ^2 x} {1\tan x}Answer (1 of 4) (tan x1)^2=(12sin xcos x)/(cos^2 x) LHS =(tan x1)^2 =(sin x/cos x1)^2 ={(sin xcos x)/cos x}^2 =(sin x cos x)^2 /(cos^2 x) =(sin^2 x cos




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




Proving Trig Identity Tan 2x Tan X Frac Tan X Cos 2x Mathematics Stack Exchange
Cos^2x(1tan^2x)=1 secxtanx(1sin^2x)=sinx cos^2(2x)sin^2=0 ** cos^2x(1tan^2x)=1 cos^2xsin^2x/cos^2x=1 cos^2xsin^2x=1 left side = right side, therefore, equation is an identity secxtanx(1sin^2x)=sinx (1/cosx*sinx/cosx)(11cos^2x (sinx/cos^2x)(cos^2x)=sinx left side = right side, therefore, equation is an identity cos^2(2x)sin^2=0 cos^2xsin^2xsin^2xAnswer (1 of 6) I know that and The next step would then be to say that but now what?BSc in Theoretical Physics & Mathematical Physics, Heidelberg University (Graduated ) tan^2x/ (1tan^2x) WolframAlpha As you can see it comes out to sin^2 (x) You can see this yourself by reminding yourself of the definition of tan (x) and then using the identity sin^2 (x)cos^2 (x) = 1
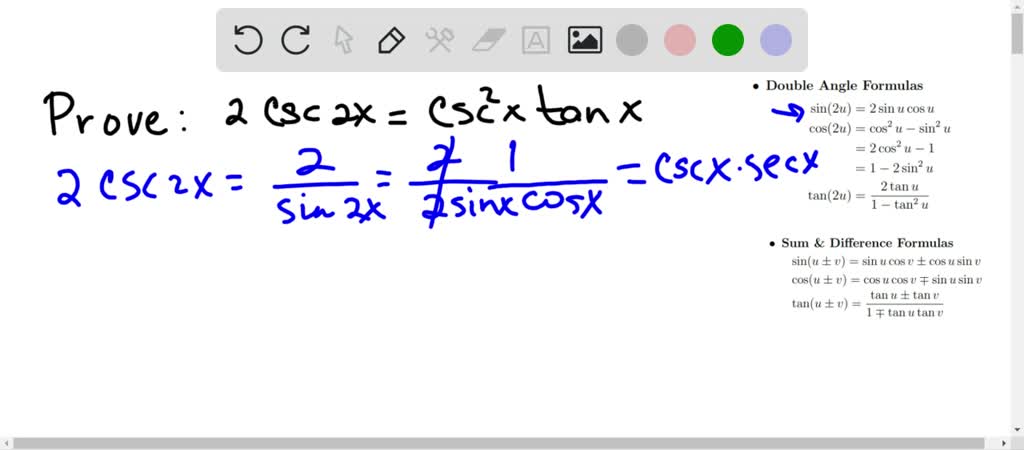



Solved In Exercises 15 22 Prove The Identity 2 Csc 2 X Csc 2 X Tan X




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube
0 points Verify that each equation is an identitycos4 x =Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x)Pythagorean identities are identities in trigonometry that are extensions of the Pythagorean theorem The fundamental identity states that for any angle θ, \theta, θ, cos 2 θ sin 2 θ = 1 \cos^2\theta\sin^2\theta=1 cos2 θsin2 θ = 1 Pythagorean identities are useful in simplifying trigonometric expressions, especially in




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Integrate Sec 2x Method 1
Verify this identity (tan^2(x)1)/(1tan^2(x)) = 12cos^2(x) ~~~~~ It is done in 3 (three) easy steps 1 The numerator tan^2(x) 1 = = (1) 2 The denominator 1 tan^2(x) = = = (2) 3Sin (x y) = sin x cos y cos x sin y cos (x y) = cos x cosy sin x sin y tan (x y) = (tan x tan y) / (1 tan x tan y) sin (2x) = 2 sin x cos x cos (2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan (2x) = 2 tan (x) / (1 tan 2 (x)) sin 2 (x) = 1/2 1/2 cos (2x) cos 2 (x) = 1/2 1/2 cos (2x) sin x sin y = 2 sin ( (x y)/2 ) cos ( (x y)/2 ) Divide both side by cos^2x and we get sin^2x/cos^2x cos^2x/cos^2x = 1/cos^2x tan^2x 1 = sec^2x tan^2x = sec^2x 1 Confirming that the result is an identity




Solve Tan 2 X 1 0 Yahoo Answers Noha Matthieu Lire Un Livre




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube
Answer to Prove the identity {1 tan^2 x} / {sin^2 x cos^2x} = sec^2 x By signing up, you'll get thousands of stepbystep solutions to yourExcellent application of Pythagorean Trig Identities email anilanilkhandelwal@gmailcom
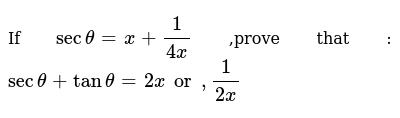



The Equation Sec 2x 1 Tan 2x Is An Identity True Or False



Bestmaths Online Proof 4




bestpictjcry Tan 2x Tan 2x
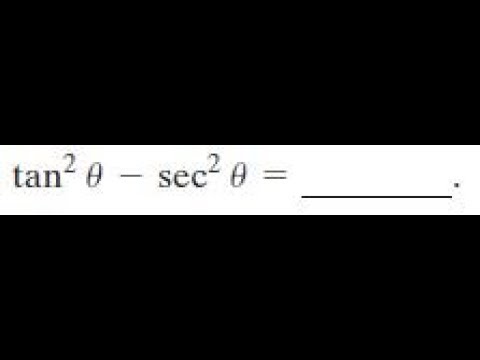



Tan 2x Sec 2x Youtube



Prove Sin2x 2tanx 1 Tan 2x Socratic
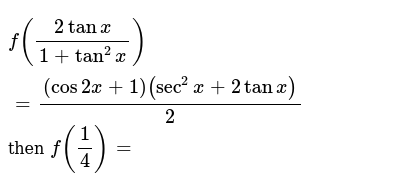



いろいろ Tan2x 1sec2x ただの悪魔の画像
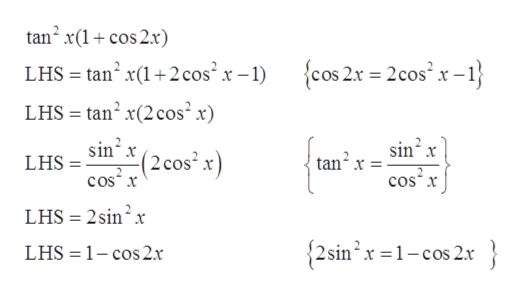



Answered Tan2x 1 Cos2x 1 Cos2x Verify The Bartleby




上 Tan2x Identity ただの悪魔の画像



Prove The Identity Secxcscx Tanx Cotx 2 Tan 2x Cot 2x1 Apply The Distributive Property2 Apply The Brainly Com
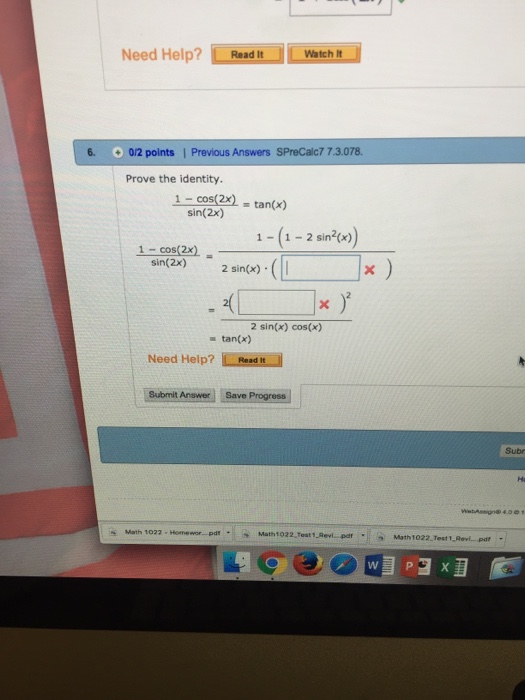



Solved Prove The Identity 1 Cos 2x Sin 2x Tan X 1 Chegg Com




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic



bestpictjcry Tan 2x Tan 2x




Solved Question 1 Prove The Following Trigonometric Identities Sin2i Cos2i 1 2 Cos2i Tan2i 1 1cos2i Sini Tani Cosi 1cosi Tan2xsin2x 1 Tan2x Cos2x 1 Tan2x 1 Sinx1 Tanx Tanxsinx Cosx Sinx Cosxsinx Cosx Sin4x Cos4x Tanx Cotxtan2x Cot2x




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



A Trig Identity




Trig Identity Sec2x Minus Tan2x T10 Youtube




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities



How To Show That Math Tan 2 X Sec 2 X 1 Math Quora




Solved Verify The Identity 4 2 Tan X Secx2tan X 1 Which Chegg Com



True Or False The Equation Sec 2 X 1 Tan 2 X Is An Identity Brainly Com
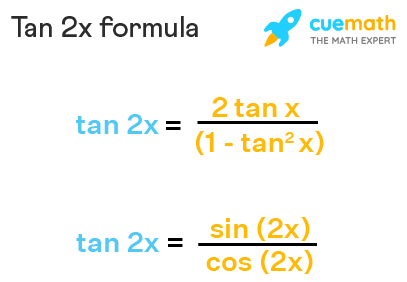



Tan 2x Formula What Is Tan 2x Formula Examples



Fastest Is Tan 2x Cot 2x 1 An Identity




Ch Ppt Download
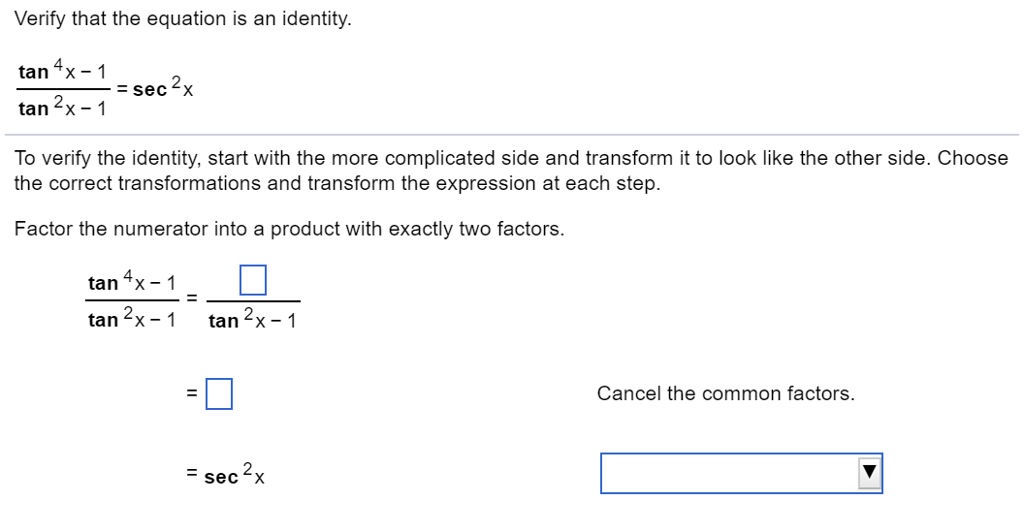



Solved Verify That The Equation Is An Identity Tan 4x 1 Chegg Com




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic



1 Tan 2x Sec 2x
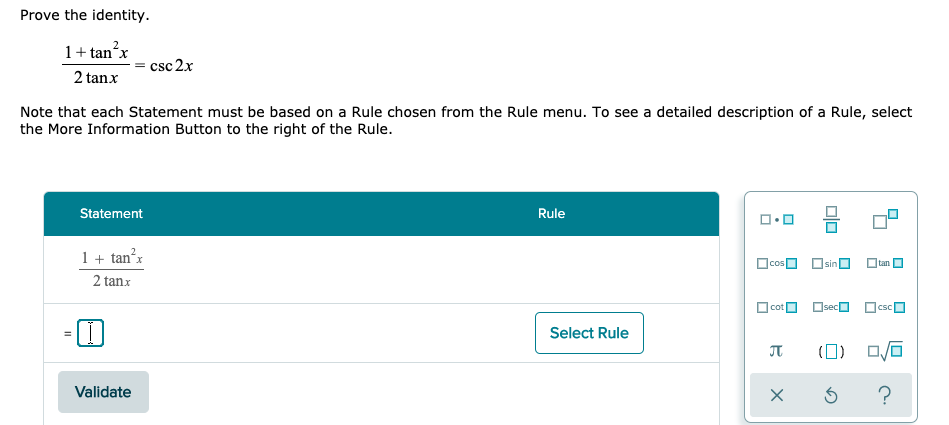



Solved Prove The Identity 1 Tan X 2 Tanx Csc 2x Note Chegg Com




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi



Ilectureonline




Solved Verify That The Equation Is An Identity Tan 2x Cot Chegg Com




Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby




Weierstrass Substitution Wikipedia




Proof Tan 2 1 Sec 2 Youtube




How Do You Prove Tan 2x Secx 1 1 Secx Socratic



1



Dxyot5v7ekyzfm
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com




Get Answer 1 Tan2x Sec2x Dx Sin2x 2 C Tan 2 X 2 C 2sin X Cos X Transtutors



What Is The Formula Of Tan2x Quora




Tan 2x Formula What Is Tan 2x Formula Examples




Trig Double Identities Trigonometric Double Angle Functions Trig



Solved Review The Following Derivation Of The Tangent Double Angle Identity The Steps Are Not Listed In The Correct Order Course Hero
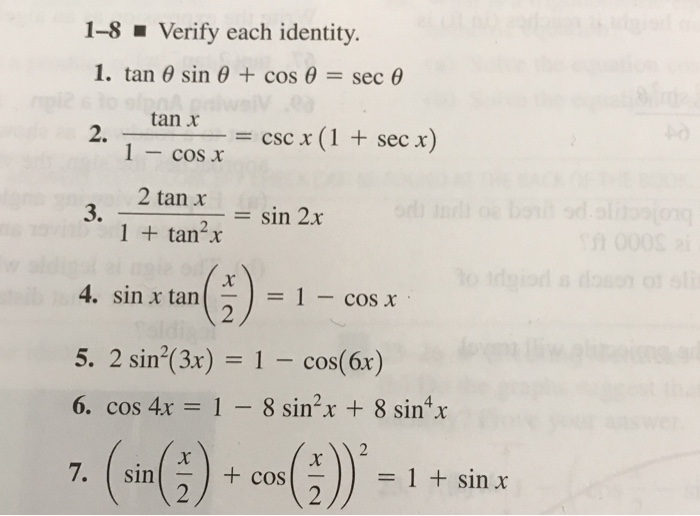



Solved 1 8 Verify Each Identity Sec 8 1 Tan 8 Sin 8 Chegg Com




Answered Verify The Identity 2 Tan X 1 Bartleby




Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




O Trigonometric Identities And Equations Double Angle Identities Problem Type 1 3 Find Sin 2x Cos 2x Homeworklib




Using Trigonometric Identities Video Khan Academy
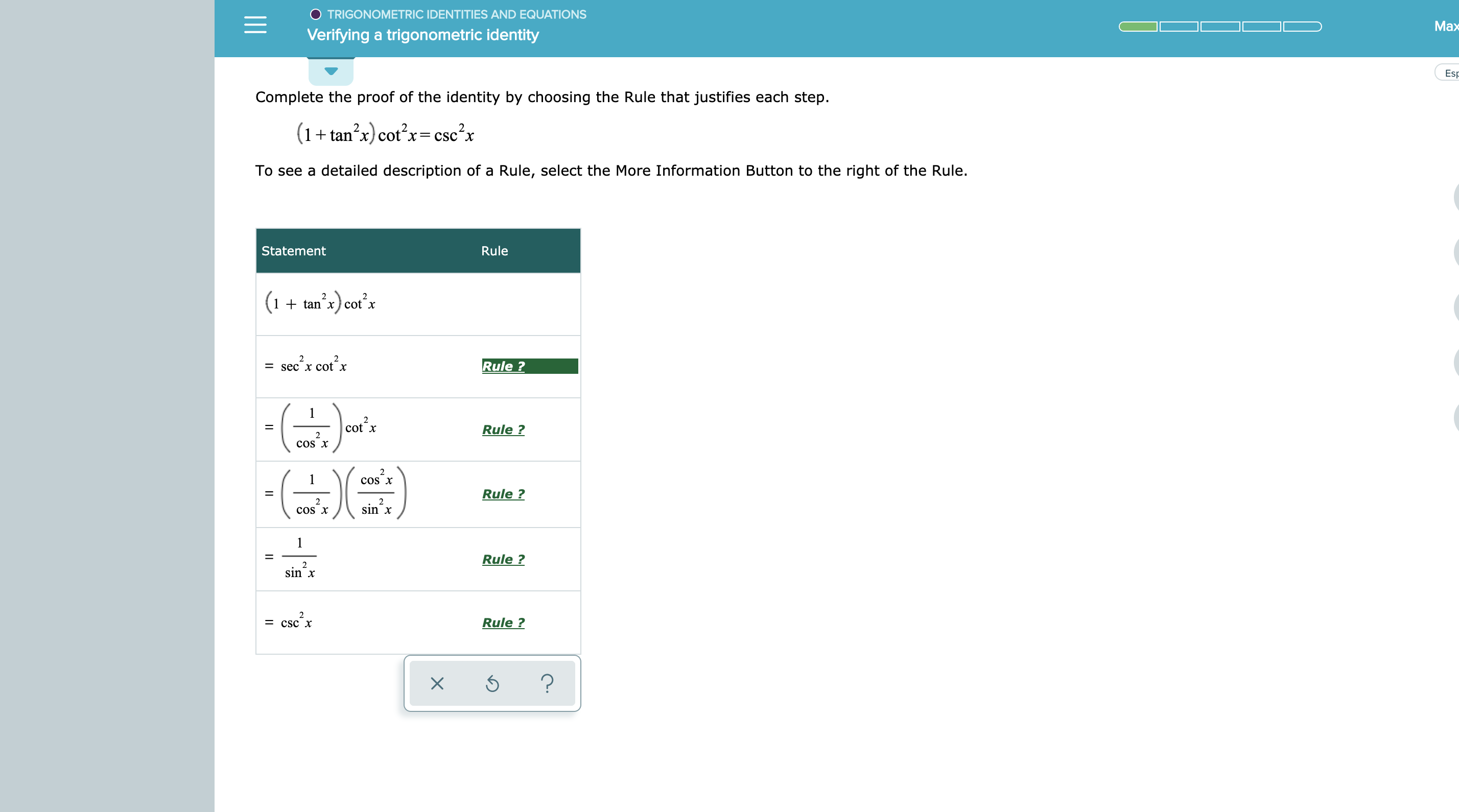



Answered Trigonometric Identities And Equations Bartleby




Sin2x Cos2x 1 Proof




Prove The Identity 1 Tan 2x 1 Tan 2x 1 2sin 2x In Urdu Hindi Youtube




いろいろ Tan2x 1sec2x ただの悪魔の画像



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero




Answered 1 8 Verify Each Identity 1 Tan 0 Bartleby



Sin 2 X Cos 2 X 1 Alvina Spike




Integrate Tan 2x




Tangent Half Angle Formula Wikipedia




Analytic Trig Ppt Video Online Download




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Homeworklib



3




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube




9 1 Identities And Proofs Ppt Download



How To Show That Math Tan 2 X Sec 2 X 1 Math Quora




Which Of The Following Equations Are Identities Check All That Apply A Cot 2x Csc2x 1 B Brainly Com




Solved Verify The Identity 2 Tan X Sin 2x 1 Tan2 X 2 Chegg Com



Solution Tan 2x Secx 1 1 Cosx Cosx Please And Thank You




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Homeworklib




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Ch 7 Trigonometric Identities And Equations Ppt Video Online Download
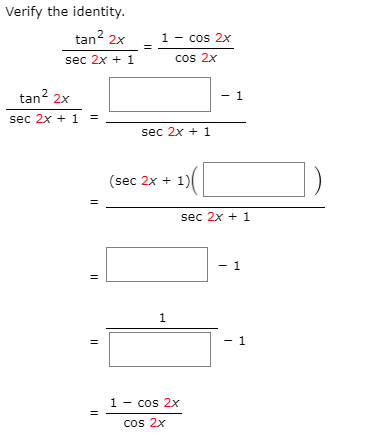



Solved Verify The Identity Tan 2x 1 Cos 2x Cos 2x Sec 2x Chegg Com



What Would Be Steps In Proving That Tan2x Secx 1 1 Sec X Socratic



1 Point If Tan X 1 3 Cosx 0 Then Sin 2x Cos 2x Homeworklib




上 Tan2x Identity ただの悪魔の画像



0 件のコメント:
コメントを投稿